Bayesian Modeling

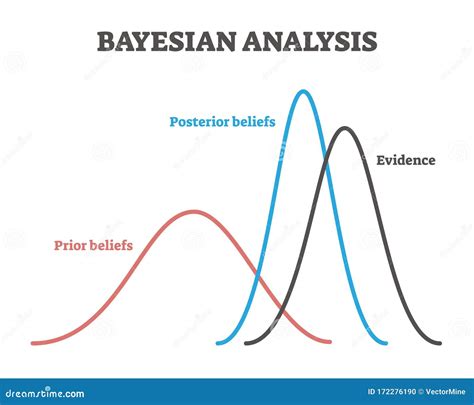
The Power of Bayesian Modeling: A Comprehensive Guide

In the realm of data analysis and statistical inference, Bayesian modeling has emerged as a powerful tool, offering a unique and versatile approach to understanding complex data. This article aims to delve into the world of Bayesian modeling, exploring its principles, applications, and the profound impact it has on various fields. From its historical roots to its modern-day implementations, we will uncover the intricacies of this statistical framework and its ability to revolutionize decision-making processes.

At its core, Bayesian modeling represents a paradigm shift in statistical thinking, providing a more intuitive and flexible method for updating beliefs based on new evidence. Unlike traditional frequentist approaches, Bayesian inference assigns probabilities to hypotheses or parameters, allowing for a more dynamic and personalized understanding of data. This shift in perspective has opened up new avenues for exploration and has become an indispensable tool in a wide range of disciplines, including machine learning, healthcare, finance, and beyond.

Understanding the Bayesian Framework

Bayesian modeling is named after the Reverend Thomas Bayes, an 18th-century statistician and philosopher who developed the foundational theorem that underpins this approach. The Bayesian framework is built upon the concept of conditional probability, where the probability of an event is updated based on the occurrence of another event. This fundamental principle, known as Bayes' theorem, forms the basis for all Bayesian analyses.

At its simplest, Bayes' theorem can be expressed as follows:

P(A|B) = P(B|A) * P(A) / P(B)

Here, P(A|B) represents the probability of event A occurring given that event B has occurred. P(B|A) is the probability of event B given A, P(A) is the prior probability of event A, and P(B) is the probability of event B. This theorem allows us to update our beliefs about an event based on new information, a process known as Bayesian updating.

The Bayesian Workflow

The Bayesian workflow typically involves a series of steps, each contributing to the overall analysis. Here's a simplified breakdown of the process:

1. Define the Problem: Clearly articulate the research question or objective. This step involves identifying the variables of interest and understanding the data collection process.
2. Specify the Prior: Choose an appropriate prior distribution that represents your initial belief about the parameters. This prior can be based on existing knowledge, expert opinion, or previous studies.
3. Design the Model: Develop a mathematical model that describes the relationship between the variables and the data. This model should be based on the problem definition and the underlying assumptions.
4. Collect Data: Gather relevant data that aligns with the model and the research question. This step may involve experimental design, data collection, or data extraction from existing sources.
5. Update the Prior: Use Bayes' theorem to update the prior distribution based on the observed data. This results in a posterior distribution, which represents the updated belief about the parameters.
6. Analyze and Interpret: Perform statistical analysis on the posterior distribution to extract meaningful insights. This may involve computing summary statistics, visualizing the results, and drawing conclusions.
7. Communicate Findings: Effectively convey the results and their implications to stakeholders or the wider scientific community. This step is crucial for ensuring the impact and applicability of the analysis.

Applications and Impact

The versatility of Bayesian modeling has led to its widespread adoption across numerous fields. Here, we explore some of the key areas where Bayesian inference has made a significant impact.

Machine Learning and Artificial Intelligence

Bayesian modeling has become a cornerstone in machine learning, particularly in areas such as probabilistic programming, deep learning, and reinforcement learning. By treating model parameters as random variables, Bayesian methods allow for a more flexible and robust approach to training and inference. This has led to advancements in areas like natural language processing, computer vision, and autonomous systems.

Healthcare and Clinical Trials

In healthcare, Bayesian modeling has revolutionized clinical trials and medical decision-making. By incorporating prior knowledge and updating beliefs based on new patient data, Bayesian methods provide a more personalized approach to treatment. This has been particularly beneficial in areas like drug development, where Bayesian models can guide dosage decisions and optimize treatment protocols.

Finance and Risk Management

The financial industry has embraced Bayesian modeling for its ability to handle complex and uncertain scenarios. Bayesian methods are used in areas such as portfolio optimization, credit risk assessment, and pricing derivatives. By incorporating market data and expert knowledge, Bayesian models provide a more robust framework for risk management and investment strategies.

Environmental Science and Ecology

Bayesian modeling has played a crucial role in ecological research and environmental monitoring. By integrating data from various sources, such as satellite imagery, field surveys, and sensor data, Bayesian methods allow for a more comprehensive understanding of ecological systems. This has led to advancements in areas like biodiversity assessment, habitat modeling, and climate change impact studies.

Real-World Examples and Case Studies

To illustrate the power of Bayesian modeling, let's explore some real-world examples and case studies where Bayesian methods have made a significant impact.

Case Study: Climate Change Modeling

In the field of climate science, Bayesian modeling has been used to improve the accuracy of climate change projections. By incorporating prior knowledge about climate dynamics and updating beliefs based on observational data, Bayesian models provide a more robust framework for understanding complex climate systems. This has led to more accurate predictions of temperature trends, sea level rise, and extreme weather events.

Case Study: Drug Discovery

Bayesian modeling has revolutionized drug discovery by providing a more efficient and targeted approach. By using Bayesian methods to analyze large datasets of chemical compounds and biological assays, researchers can identify potential drug candidates with greater accuracy. This has accelerated the drug development process and increased the likelihood of successful clinical trials.

Case Study: Personalized Medicine

In the realm of personalized medicine, Bayesian modeling has been instrumental in developing tailored treatment plans for individual patients. By incorporating patient-specific data, such as genetic profiles and medical histories, Bayesian models can provide personalized recommendations for dosage, treatment duration, and drug combinations. This has improved patient outcomes and reduced the risk of adverse effects.

Challenges and Considerations

While Bayesian modeling offers numerous advantages, it is not without its challenges. Some key considerations and potential pitfalls include:

• Computational Complexity: Bayesian analyses often involve complex computations, especially when dealing with high-dimensional data or hierarchical models. This can require significant computational resources and specialized software.
• Choice of Prior: The choice of prior distribution can have a significant impact on the results. An inappropriate or poorly chosen prior can lead to biased estimates or incorrect conclusions. Careful consideration and justification of the prior are essential.
• Data Requirements: Bayesian methods often require larger datasets to provide reliable results. In cases where data is limited or sparse, Bayesian models may struggle to provide accurate inferences.
• Interpretability: While Bayesian models can provide rich and detailed inferences, interpreting these results can be challenging, especially for complex models. Effective communication and visualization techniques are crucial for conveying the insights to stakeholders.

Future Implications and Advancements

The field of Bayesian modeling continues to evolve, driven by advancements in technology and an increasing demand for more sophisticated statistical methods. Here are some key areas where we can expect further developments:

• Scalability and Efficiency: Researchers are actively working on developing more scalable and efficient algorithms for Bayesian inference. This includes advancements in variational inference, approximate Bayesian computation, and parallel computing techniques.
• Integrating Deep Learning: The integration of deep learning and Bayesian methods is an emerging area of research. By combining the flexibility of Bayesian models with the power of deep neural networks, researchers aim to develop more robust and accurate predictive models.
• Causal Inference: Bayesian modeling has the potential to enhance causal inference, allowing researchers to better understand the underlying mechanisms that drive observed phenomena. This has implications for fields such as epidemiology, economics, and social sciences.
• Bayesian Ethics and Fairness: As Bayesian modeling becomes more prevalent, there is a growing focus on ethical considerations. Researchers are exploring ways to ensure that Bayesian models are fair, unbiased, and respect individual privacy and autonomy.

Conclusion

Bayesian modeling has emerged as a powerful tool, revolutionizing the way we approach statistical inference and decision-making. Its ability to incorporate prior knowledge, update beliefs based on new evidence, and provide personalized insights has made it an indispensable tool across a wide range of disciplines. As we continue to explore the potential of Bayesian methods, we can expect further advancements and a deeper understanding of complex data and phenomena.