Dynamic Programming Algorithm
Dynamic programming is a powerful algorithmic technique that solves complex problems by breaking them down into simpler subproblems and solving each subproblem only once. It is particularly useful for optimization problems where the goal is to find the most efficient solution among many possible alternatives. This article explores the fundamentals of dynamic programming, its applications, and real-world examples to demonstrate its significance and impact.
Understanding Dynamic Programming

Dynamic programming, often referred to as DP, is a method that transforms complex problems into a sequence of simpler problems. It is based on the principle of optimality, which states that an optimal solution to a problem can be constructed from optimal solutions to its subproblems. By storing and reusing the solutions to these subproblems, dynamic programming avoids the trap of solving the same subproblem repeatedly, thereby improving computational efficiency.
The core idea behind dynamic programming is to build up solutions to larger problems by combining solutions to smaller, overlapping subproblems. This approach is especially effective for problems that exhibit optimal substructure and overlapping subproblems. Optimal substructure means that the optimal solution to a problem can be derived from the optimal solutions of its subproblems. Overlapping subproblems, on the other hand, occur when multiple subproblems share common subproblems.
By utilizing dynamic programming, programmers can tackle a wide range of problems in various domains, including computer science, operations research, economics, and more. It provides a systematic way to approach and solve problems that may seem daunting at first glance. Let's delve deeper into the key concepts and applications of dynamic programming.
Key Concepts in Dynamic Programming

Optimal Substructure
Optimal substructure is a fundamental concept in dynamic programming. It states that a problem can be divided into smaller, optimal subproblems, and the optimal solution to the original problem can be constructed from these subproblem solutions. This property allows dynamic programming algorithms to build up solutions iteratively, ensuring that the overall solution is optimal.
For example, consider the Fibonacci sequence, where each number is the sum of the two preceding ones. To find the nth Fibonacci number, we can break down the problem into smaller subproblems, calculating each Fibonacci number from its previous two values. By storing and reusing these subproblem solutions, we can efficiently compute the nth Fibonacci number without recalculating intermediate results.
Overlapping Subproblems
Overlapping subproblems occur when solving a problem leads to the repetition of similar or identical subproblems. In dynamic programming, identifying and avoiding the repetition of subproblems is crucial for improving computational efficiency. By storing the solutions to overlapping subproblems, we can quickly retrieve the results without recomputing them.
A classic example of overlapping subproblems is the longest common subsequence problem, where we aim to find the longest sequence common to two given sequences. By using dynamic programming, we can create a table that stores the length of the longest common subsequence for various subproblems, avoiding the need to recalculate the same subproblem multiple times.
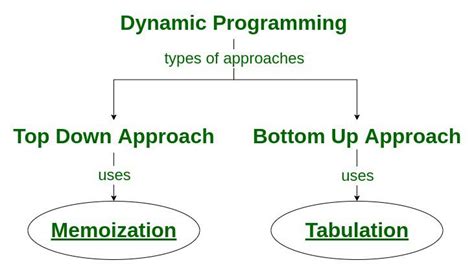
Memoization
Memoization is a technique used in dynamic programming to store and reuse the solutions to subproblems. It involves creating a memo, which is a data structure that holds the results of previously solved subproblems. When a subproblem is encountered, the memo is checked first to see if the solution already exists. If it does, the stored solution is retrieved; otherwise, the subproblem is solved, and its solution is stored in the memo for future reference.
Memoization significantly reduces the time complexity of dynamic programming algorithms by avoiding redundant calculations. It is particularly effective for problems with a large number of overlapping subproblems, where storing and retrieving solutions can lead to substantial performance improvements.
Applications of Dynamic Programming
Knapsack Problem
The knapsack problem is a classic optimization problem in which we have a set of items, each with a weight and a value, and we aim to maximize the total value while staying within a given weight limit. Dynamic programming provides an efficient solution to this problem by breaking it down into smaller subproblems and using memoization to store and retrieve solutions.
By creating a table that represents the maximum value that can be obtained for different weight limits, we can iteratively build up the solution. Each cell in the table stores the maximum value achievable for a given weight limit, and the table is filled in a bottom-up manner, ensuring that we consider all possible combinations of items.
Shortest Path Algorithms
Dynamic programming is widely used in shortest path algorithms, such as Dijkstra’s algorithm and the Bellman-Ford algorithm. These algorithms aim to find the shortest path between two nodes in a graph. By applying dynamic programming, we can efficiently compute the shortest path by breaking the problem down into subproblems and storing the results in a data structure, such as a priority queue.
For example, Dijkstra's algorithm uses a priority queue to store the shortest distance from the source node to each visited node. By repeatedly selecting the node with the minimum distance from the source and updating the distances of its neighbors, we can find the shortest path to all reachable nodes.
String Matching and Sequence Alignment
Dynamic programming is invaluable in string matching and sequence alignment problems, which are common in bioinformatics and text processing. These problems involve finding the best alignment between two sequences, such as DNA or protein sequences, or comparing two strings to identify similarities.
By creating a dynamic programming table that represents the optimal alignment for different subproblems, we can efficiently compute the global alignment between the sequences. The table is filled by comparing the characters at corresponding positions and updating the alignment scores based on the best matches, gaps, or mismatches.
Resource Allocation and Scheduling
Dynamic programming is applied in various resource allocation and scheduling problems, such as job scheduling, project management, and resource optimization. These problems often involve making a sequence of decisions to maximize some objective while considering constraints and limitations.
For instance, in job scheduling, dynamic programming can be used to determine the optimal order in which jobs should be executed to minimize the total completion time or maximize the overall profit. By breaking the problem into smaller subproblems and considering the dependencies between jobs, we can find the optimal schedule that satisfies the given constraints.
Performance Analysis and Comparison
Dynamic programming algorithms offer significant advantages over naive brute-force approaches in terms of time and space complexity. By solving subproblems only once and reusing their solutions, dynamic programming reduces the overall computational effort. This is particularly beneficial for problems with a large search space or exponential complexity.
| Algorithm | Time Complexity | Space Complexity |
|---|---|---|
| Naive Brute-Force | O(2^n) | O(1) |
| Dynamic Programming | O(n^2) or O(n^3) | O(n) or O(n^2) |
As illustrated in the table above, dynamic programming algorithms often have a lower time complexity compared to naive brute-force approaches. While the exact time and space complexity depends on the specific problem and algorithm, dynamic programming generally offers a more efficient solution, especially for larger inputs.
Real-World Examples and Impact

Route Planning and Navigation
Dynamic programming plays a crucial role in route planning and navigation systems. By using algorithms like the A* search algorithm, which incorporates dynamic programming principles, navigation apps can efficiently calculate the shortest path between two locations while considering various factors such as traffic, road conditions, and user preferences.
These algorithms break down the problem of finding the optimal route into smaller subproblems, each representing a sequence of road segments. By storing and reusing the solutions to these subproblems, navigation systems can quickly determine the best route, providing users with accurate and efficient travel guidance.
Financial Portfolio Optimization
In the financial industry, dynamic programming is used to optimize investment portfolios and make informed trading decisions. By applying dynamic programming algorithms, financial analysts and traders can determine the optimal allocation of assets to maximize returns while considering risk factors and market dynamics.
For example, the Markowitz portfolio optimization problem aims to find the combination of assets that maximizes the expected return for a given level of risk. Dynamic programming can be employed to solve this problem by iteratively building up the optimal portfolio by considering different asset combinations and their associated risks.
Speech Recognition and Natural Language Processing
Dynamic programming techniques are integral to speech recognition and natural language processing (NLP) tasks. These algorithms, such as the Viterbi algorithm and the Hidden Markov Model (HMM), use dynamic programming to find the most likely sequence of hidden states or words that correspond to a given observation or speech signal.
By breaking down the problem into smaller subproblems and applying dynamic programming, these algorithms can efficiently compute the most probable sequence, enabling accurate speech recognition and language understanding. This has significant implications for voice assistants, language translation services, and various NLP applications.
Conclusion
Dynamic programming is a fundamental algorithmic technique that has revolutionized the way we solve complex optimization problems. By leveraging the principles of optimal substructure and overlapping subproblems, dynamic programming algorithms provide efficient solutions, often outperforming naive approaches in terms of time and space complexity. Its applications span across diverse domains, making it an indispensable tool for computer scientists, engineers, and researchers alike.
As we continue to tackle more intricate problems and explore new frontiers, dynamic programming remains a cornerstone in algorithmic design. Its impact on fields like navigation, finance, and natural language processing showcases its versatility and potential for further innovation. By understanding and applying dynamic programming, we can unlock new possibilities and drive advancements in technology and beyond.
What are some common examples of dynamic programming problems?
+Common examples include the Fibonacci sequence, longest common subsequence, knapsack problem, shortest path algorithms, and sequence alignment problems in bioinformatics.
How does dynamic programming improve computational efficiency?
+Dynamic programming improves efficiency by solving each subproblem only once and storing its solution. This avoids redundant calculations and allows for faster retrieval of results when solving overlapping subproblems.
What are the key benefits of using dynamic programming in optimization problems?
+Dynamic programming offers benefits such as reduced time complexity, improved space efficiency, and the ability to find optimal solutions to complex problems that may not be feasible with brute-force approaches.
Can dynamic programming be applied to all types of problems?
+While dynamic programming is powerful, it is most effective for problems with optimal substructure and overlapping subproblems. It may not be suitable for problems that do not exhibit these properties or for problems with highly constrained or unique characteristics.