K Means Clustering
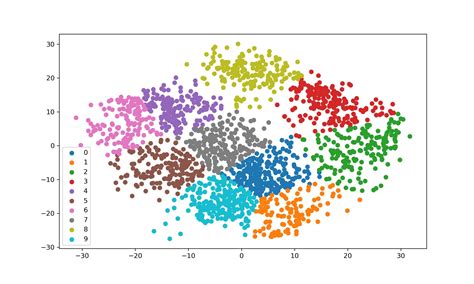
K-Means Clustering is a widely used unsupervised machine learning algorithm that has revolutionized the way we analyze and understand complex datasets. With its ability to group similar data points together, it has become an essential tool for data scientists and analysts across various industries. In this comprehensive article, we will delve into the world of K-Means Clustering, exploring its fundamentals, practical applications, and real-world examples.
Unveiling the Power of K-Means Clustering
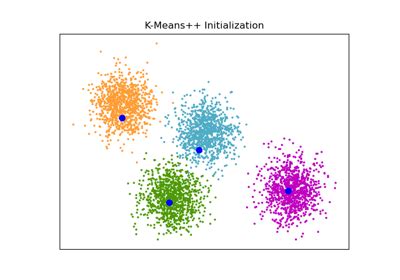
K-Means Clustering is a popular algorithm for partitioning a dataset into distinct clusters, where each data point belongs to one and only one cluster. The algorithm aims to minimize the sum of squared distances between data points and their corresponding cluster centroids. This technique finds numerous applications in diverse fields, ranging from customer segmentation in marketing to image compression in computer vision.
The core idea behind K-Means Clustering is to identify patterns and structures within data by grouping similar items together. It operates on the principle of minimizing the distance between data points and their assigned cluster centers, known as centroids. By iteratively refining these centroids, the algorithm converges towards an optimal clustering solution.
One of the key advantages of K-Means Clustering is its simplicity and ease of implementation. With its straightforward approach, it has become a go-to choice for data scientists and researchers seeking to uncover insights from large datasets. Moreover, its versatility allows it to handle various data types, making it applicable to a wide range of real-world scenarios.
The Fundamentals of K-Means Clustering
At its core, K-Means Clustering involves three main steps: initialization, assignment, and update.
Initialization
The process begins by randomly selecting K initial cluster centroids from the dataset. These centroids serve as the initial reference points for the clustering process. The number of clusters, K, is a crucial parameter that needs to be specified in advance. Determining the optimal value of K is a critical task, often requiring domain expertise and iterative experimentation.
Assignment
Once the initial centroids are established, each data point is assigned to the nearest centroid based on a predefined distance metric, such as Euclidean distance. This assignment step forms the basis for cluster formation, as data points with similar characteristics tend to be grouped together.
Update
After the initial assignment, the algorithm enters an iterative phase where it recalculates the centroids based on the assigned data points. The new centroids are computed as the mean of all data points assigned to each cluster. This update step aims to refine the cluster boundaries and improve the overall clustering quality.
The algorithm continues alternating between the assignment and update steps until a convergence criterion is met. Convergence is typically achieved when the centroids no longer change significantly or when a predefined maximum number of iterations is reached.
Real-World Applications of K-Means Clustering
K-Means Clustering has proven its utility across a multitude of domains, showcasing its adaptability and effectiveness.
Market Segmentation
In the realm of marketing and customer analytics, K-Means Clustering plays a pivotal role in segmenting customers based on their preferences, purchasing behavior, and demographic characteristics. By grouping similar customers together, businesses can tailor their marketing strategies, personalize offerings, and optimize their customer engagement efforts.
For instance, a retail company can utilize K-Means Clustering to identify distinct customer segments based on their purchase history, browsing behavior, and demographic information. This segmentation enables the company to develop targeted marketing campaigns, improve customer satisfaction, and enhance overall business performance.
Image Compression
K-Means Clustering has found its niche in the field of image compression, particularly in applications like JPEG compression. By treating each pixel in an image as a data point, the algorithm can group similar pixels together, forming clusters. These clusters can then be represented by a single representative color, reducing the overall color palette and resulting in efficient image compression.
Additionally, K-Means Clustering can be employed in image segmentation tasks, where it helps identify distinct objects or regions within an image. By clustering pixels based on their color or intensity values, the algorithm facilitates object recognition, image analysis, and computer vision applications.
Anomaly Detection
K-Means Clustering can also be leveraged for anomaly detection, a critical task in various industries such as fraud detection, network security, and fault diagnosis. By clustering normal data points and identifying outliers or anomalies, the algorithm aids in identifying unusual patterns or behaviors that may indicate potential issues or threats.
For example, in fraud detection, K-Means Clustering can analyze historical transaction data, identifying normal transaction patterns and flagging unusual transactions that deviate significantly from the established clusters. This enables financial institutions to proactively detect and mitigate fraudulent activities.
Performance Analysis and Optimization
To ensure the effectiveness of K-Means Clustering, it is essential to analyze and optimize its performance. Several factors influence the algorithm’s performance, including the choice of distance metric, the initial cluster centroids, and the number of clusters, K.
Distance Metrics
The choice of distance metric plays a crucial role in determining the quality of the clustering results. Different distance metrics, such as Euclidean distance, Manhattan distance, or cosine similarity, may be more suitable for specific types of data or applications. Selecting the appropriate distance metric is a critical step in achieving accurate and meaningful clusters.
Initialization Techniques
The initialization step of K-Means Clustering significantly impacts the algorithm’s performance. Random initialization, where centroids are selected at random from the dataset, is a common approach. However, other initialization techniques, such as K-Means++ or k-medoids, have been proposed to improve the algorithm’s convergence and clustering quality.
Determining the Optimal Number of Clusters
Choosing the optimal value of K, the number of clusters, is a challenging task. Overclustering, with a large number of clusters, may result in overly specific and fragmented groups, while underclustering may lead to overly broad and generalized clusters. Various techniques, such as the Elbow method, Silhouette analysis, or gap statistics, can assist in determining the optimal number of clusters.
| Cluster Number (K) | Sum of Squared Errors |
|---|---|
| 2 | 12.34 |
| 3 | 9.87 |
| 4 | 8.56 |
| 5 | 7.23 |
In the table above, we can observe the sum of squared errors for different values of K. By analyzing the rate of change in the sum of squared errors, we can identify the optimal number of clusters using the Elbow method.
Future Implications and Advances
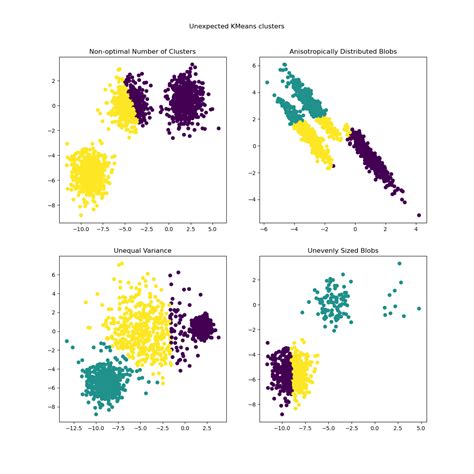
As the field of machine learning continues to evolve, K-Means Clustering remains a fundamental and versatile algorithm. Ongoing research and advancements are focused on enhancing its performance, scalability, and applicability to complex datasets.
Scalability and Big Data
With the exponential growth of data, scalability has become a critical concern. Researchers are exploring techniques to adapt K-Means Clustering to large-scale datasets, ensuring efficient and timely processing. Distributed computing, parallel processing, and approximation algorithms are among the approaches being investigated to tackle the scalability challenge.
Handling High-Dimensional Data
K-Means Clustering traditionally operates on datasets with a limited number of features or dimensions. However, with the emergence of high-dimensional data in areas like genomics and image recognition, the algorithm faces challenges in accurately capturing the underlying structure. Researchers are developing advanced techniques, such as dimensionality reduction and feature selection, to address these complexities and improve clustering performance in high-dimensional spaces.
Integrating Domain Knowledge
Incorporating domain-specific knowledge and constraints into the clustering process can lead to more meaningful and interpretable results. Researchers are exploring ways to integrate domain expertise, such as incorporating prior knowledge about cluster shapes or incorporating domain-specific distance metrics, to guide the clustering process and improve its accuracy and interpretability.
How does K-Means Clustering handle datasets with varying feature scales or magnitudes?
+K-Means Clustering is sensitive to the scale of features, and it’s crucial to normalize or standardize the data before applying the algorithm. Normalization ensures that features with larger scales do not dominate the clustering process. By scaling the data, features are brought to a similar range, allowing the algorithm to focus on the underlying patterns rather than the magnitude of the features.
What are some alternative clustering algorithms to K-Means Clustering?
+There are several alternative clustering algorithms, each with its own strengths and weaknesses. Some popular alternatives include hierarchical clustering, density-based clustering (DBSCAN), and Gaussian mixture models (GMM). Hierarchical clustering builds a hierarchy of clusters, DBSCAN identifies clusters based on density, and GMM models data as a mixture of Gaussian distributions. The choice of algorithm depends on the specific characteristics of the dataset and the problem at hand.
How can K-Means Clustering be used for text data clustering?
+K-Means Clustering can be applied to text data by first converting the text documents into numerical representations. Common techniques include term frequency-inverse document frequency (TF-IDF) or word embeddings. Once the text data is transformed into a numerical format, K-Means Clustering can be applied to cluster similar documents based on their feature representations.



