K Means Clustering Analysis
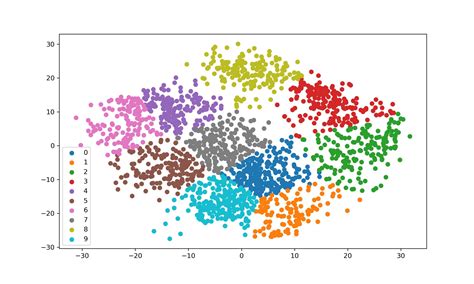
Welcome to this in-depth exploration of K-Means Clustering, a widely-used technique in data science and machine learning. In this article, we will delve into the intricacies of K-Means, its applications, and how it can be a powerful tool for understanding and analyzing complex datasets. With its ability to uncover hidden patterns and structures, K-Means Clustering has become an essential technique for data-driven decision-making across various industries.
Unveiling K-Means Clustering
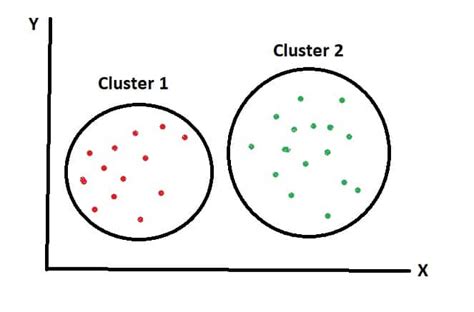
K-Means Clustering is an unsupervised machine learning algorithm that aims to group similar data points together. It is a simple yet powerful method for dividing a dataset into distinct clusters, each representing a unique group or category. The beauty of K-Means lies in its ability to discover these clusters without any prior knowledge or labels, making it an ideal choice for exploratory data analysis.
The fundamental concept behind K-Means is to minimize the distance between data points within each cluster. It achieves this by iteratively refining the cluster centroids, which represent the average of all data points within a cluster. By minimizing the sum of squared distances from each data point to its nearest centroid, K-Means ensures that similar data points are grouped together, while dissimilar points are placed in different clusters.
The K-Means Process
The K-Means algorithm follows a straightforward process, which can be summarized in the following steps:
- Initialization: Select K initial cluster centroids, either randomly or based on specific criteria. These centroids serve as the initial reference points for the clusters.
- Assignment: Assign each data point to the cluster with the nearest centroid, based on a distance metric such as Euclidean distance.
- Update: Calculate the new centroid for each cluster by taking the average of all data points assigned to that cluster.
- Repeat: Iterate between the assignment and update steps until convergence is achieved, i.e., until the cluster assignments no longer change significantly.
K-Means clustering is particularly useful when dealing with large, high-dimensional datasets, as it provides a simple and efficient way to identify underlying patterns and structures. By reducing the complexity of the data, K-Means allows for easier interpretation and decision-making.
Applications of K-Means Clustering
The versatility of K-Means clustering makes it applicable to a wide range of domains and use cases. Here are some notable applications where K-Means has proven to be invaluable:
Market Segmentation
In the realm of marketing and customer analytics, K-Means clustering is a powerful tool for market segmentation. By analyzing customer data, such as purchase history, demographics, and preferences, K-Means can identify distinct customer segments. This segmentation allows businesses to tailor their marketing strategies and product offerings to specific customer groups, leading to more effective and personalized marketing campaigns.
Image and Pattern Recognition
K-Means clustering has found extensive use in image and pattern recognition tasks. By representing images as feature vectors and applying K-Means, it is possible to group similar images together based on their visual characteristics. This technique has applications in image retrieval systems, object recognition, and even in medical imaging for disease diagnosis.
Customer Churn Prediction
Telecom and subscription-based businesses often face the challenge of customer churn, where customers cancel their subscriptions. K-Means clustering can help identify patterns and behaviors that lead to churn. By analyzing customer data, such as usage patterns, payment history, and support interactions, K-Means can segment customers into different risk groups, allowing businesses to take proactive measures to retain high-value customers.
Anomalies and Outlier Detection
K-Means clustering can also be used to detect anomalies and outliers in datasets. By identifying clusters that deviate significantly from the norm, it is possible to flag potential anomalies. This application is particularly useful in fraud detection, where unusual transaction patterns can indicate fraudulent activities. Additionally, K-Means can help identify outliers in sensor data, medical records, or financial datasets, providing valuable insights for further investigation.
Performance and Considerations
While K-Means clustering is a robust and widely-used technique, it does come with certain considerations and limitations. One of the key challenges is determining the optimal number of clusters, K. Choosing an inappropriate value of K can lead to overfitting or underfitting of the data, affecting the quality of the clustering results. Various methods, such as the elbow method or silhouette analysis, can be employed to aid in selecting the appropriate number of clusters.
Another consideration is the choice of distance metric. While Euclidean distance is commonly used, other distance metrics like Manhattan distance or cosine similarity may be more suitable for specific types of data. The choice of distance metric depends on the nature of the data and the problem at hand.
Scalability and Efficiency
K-Means clustering is known for its scalability and efficiency, making it suitable for large datasets. However, as the dataset size increases, the computational complexity also grows. Several optimization techniques, such as mini-batch K-Means and parallel computing, can be employed to enhance the performance and reduce the computational burden.
Data Preprocessing and Normalization
Effective data preprocessing is crucial for the success of K-Means clustering. Data normalization, which scales the features to a common range, ensures that no single feature dominates the clustering process. Additionally, handling missing data, outliers, and noise is essential to obtain meaningful and reliable clusters.
Comparative Analysis with Other Clustering Techniques
K-Means clustering is just one of the many clustering techniques available. While it is a popular choice due to its simplicity and efficiency, other clustering methods offer different advantages and are suitable for specific scenarios. Here’s a comparative analysis of K-Means with some alternative clustering techniques:
Hierarchical Clustering
Hierarchical clustering, unlike K-Means, does not require specifying the number of clusters beforehand. It creates a hierarchy of clusters, either in a bottom-up (agglomerative) or top-down (divisive) manner. Hierarchical clustering is useful when the dataset is hierarchical in nature or when the number of clusters is unknown. However, it can be computationally intensive for large datasets and may not provide the same level of interpretability as K-Means.
DBSCAN Clustering
Density-based spatial clustering of applications with noise (DBSCAN) is another popular clustering technique. DBSCAN identifies clusters based on the density of data points, without requiring the specification of the number of clusters. It is particularly effective for datasets with varying densities and can handle outliers and noise. However, DBSCAN may struggle with high-dimensional data and requires careful selection of density-related parameters.
Gaussian Mixture Models (GMM)
Gaussian Mixture Models (GMM) is a probabilistic approach to clustering. It assumes that the data is generated from a mixture of Gaussian distributions and aims to find the best fit for these distributions. GMM provides probabilistic cluster assignments and can handle overlapping clusters. However, it is more complex to implement and may require more computational resources compared to K-Means.
Future Implications and Advances
The field of clustering algorithms, including K-Means, is continuously evolving, driven by advancements in machine learning and data science. Here are some potential future developments and implications for K-Means clustering:
Deep Learning Integration
The integration of deep learning techniques with K-Means clustering is an exciting prospect. By combining the feature extraction capabilities of deep neural networks with the clustering power of K-Means, it may be possible to achieve more accurate and robust clustering results, especially for high-dimensional and complex datasets.
Domain-Specific Adaptations
K-Means clustering can be further specialized for specific domains and applications. By incorporating domain-specific knowledge and constraints, it is possible to develop tailored versions of K-Means that are optimized for specific use cases, such as medical imaging, natural language processing, or financial analysis.
Interactive Clustering
Interactive clustering, where users can provide feedback and guide the clustering process, is an emerging area of research. By allowing users to interact with the clustering results and provide additional context or constraints, it becomes possible to obtain more meaningful and interpretable clusters. This approach can be particularly valuable in domains where domain expertise is crucial, such as medical diagnosis or financial risk assessment.
Scalability and Distributed Computing
With the ever-increasing size of datasets, scalability and distributed computing will become even more critical for clustering algorithms like K-Means. Further research and development in this area will enable the efficient processing of massive datasets, ensuring that K-Means remains a viable option for big data analytics.
How does K-Means clustering handle datasets with varying densities and outliers?
+K-Means clustering may struggle with datasets that have varying densities or contain outliers. The presence of outliers can significantly impact the cluster centroids and potentially distort the clustering results. To mitigate this issue, it is important to preprocess the data by identifying and handling outliers before applying K-Means. Additionally, techniques like DBSCAN or density-based clustering can be more suitable for such datasets.
What are some best practices for selecting the optimal number of clusters (K) in K-Means clustering?
+Determining the optimal number of clusters is a critical step in K-Means clustering. There are several methods to aid in this process, such as the elbow method, silhouette analysis, and gap statistic. The elbow method involves plotting the within-cluster sum of squares (WSS) against different values of K and selecting the “elbow” point, where the decrease in WSS starts to level off. Silhouette analysis assesses the quality of each data point’s assignment to a cluster by measuring how similar it is to its own cluster compared to other clusters. The gap statistic compares the total within-cluster variation to that expected under a reference null distribution.
Can K-Means clustering be used for online learning or streaming data?
+Yes, K-Means clustering can be adapted for online learning or streaming data scenarios. Techniques like mini-batch K-Means or incremental K-Means can be employed to handle data that arrives sequentially or in batches. These methods update the cluster centroids incrementally, allowing for efficient clustering of large-scale streaming data.
Are there any variations of K-Means clustering that handle categorical data?
+Yes, there are variations of K-Means clustering that can handle categorical data. One such variation is the k-modes clustering algorithm, which is specifically designed for clustering categorical data. k-modes uses modes (the most frequent values) instead of means (averages) to represent the centroids of the clusters. This algorithm is particularly useful when dealing with datasets where the features are primarily categorical, such as market basket analysis or text clustering.
What are some potential challenges and limitations of K-Means clustering?
+K-Means clustering has several challenges and limitations. One of the main challenges is the sensitivity to initial cluster centroids. The quality of the clustering results can vary significantly depending on the initial placement of the centroids. Additionally, K-Means assumes that clusters are spherical and of equal variance, which may not always be the case in real-world datasets. It also struggles with datasets that have overlapping or non-convex clusters. Lastly, K-Means is not suitable for hierarchical or hierarchical-like datasets, as it does not inherently capture such structures.