Roc Specificity Sensitivity
Welcome to an in-depth exploration of the crucial concepts of specificity and sensitivity in the realm of ROC (Receiver Operating Characteristic) analysis, a fundamental aspect of medical diagnosis and predictive modeling. This article aims to delve into the intricacies of these concepts, offering a comprehensive understanding of their role and significance.
In the complex landscape of healthcare diagnostics and machine learning, the concepts of specificity and sensitivity are often the cornerstone of decision-making. They provide the foundation for interpreting test results, guiding clinical judgments, and shaping predictive models. Understanding these concepts is not just academically interesting; it is a vital skill for anyone involved in medical research, clinical practice, or data-driven decision-making.
Unraveling the ROC: A Brief Overview

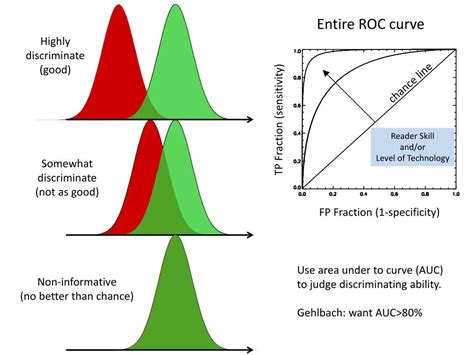
The ROC curve, a graphical representation of the performance of a binary classifier system as its discrimination threshold is varied, has been a cornerstone in various fields, from medicine to machine learning. At its core, the ROC curve offers a visual depiction of the trade-off between the true positive rate (sensitivity) and the false positive rate (1 - specificity) across a range of classification thresholds. This tool is particularly valuable when dealing with binary classification problems, where the goal is to differentiate between two distinct classes or conditions.
However, the utility of the ROC curve extends beyond its visual representation. It serves as a powerful analytical tool, offering insights into the performance and diagnostic accuracy of a system. By plotting the true positive rate against the false positive rate, the ROC curve allows for a nuanced understanding of a classifier's capabilities and limitations. This is especially critical in medical diagnostics, where the balance between true positives and false positives can have significant implications for patient care and outcome.
Specificity: Guarding Against False Alarms

Specificity, a critical metric in diagnostic testing, refers to the ability of a test to correctly identify individuals who do not have the condition of interest. In essence, it measures the proportion of true negatives out of all individuals who were correctly classified as negative. This metric is a vital indicator of a test’s precision, as it quantifies the likelihood of correctly identifying individuals who are truly disease-free.
In the context of medical diagnosis, specificity is akin to the concept of "true negative rate". It represents the probability that a test will correctly identify a person who does not have the disease as negative. For instance, if a test has a specificity of 95%, it means that for every 100 individuals who do not have the disease, the test will correctly identify 95 of them as disease-free.
Mathematically, specificity can be expressed as:
| Specificity | True Negative |
|---|---|
| Specificity = | TN / (TN + FP) |

Here, TN represents the number of true negatives, and FP represents the number of false positives. This equation highlights the direct relationship between specificity and the accuracy of a test in identifying individuals who are truly disease-free.
In the realm of predictive modeling, specificity plays a crucial role in mitigating false positives. A high specificity value indicates a lower likelihood of false positives, which can be crucial in scenarios where false positives could lead to unnecessary interventions or incorrect diagnoses. For example, in cancer screening, a test with high specificity is desirable to avoid falsely identifying healthy individuals as having cancer.
The Impact of Specificity in Clinical Practice
Specificity is not merely a theoretical concept; it has tangible implications in clinical practice. In diagnostic tests, a high specificity can lead to more accurate and reliable results, particularly in ruling out certain conditions. This is especially crucial when the consequences of a false positive could be significant, such as unnecessary treatments, increased healthcare costs, or patient anxiety.
For instance, consider a diagnostic test for a rare disease. A high specificity ensures that a positive result is more likely to be an accurate indicator of the disease's presence. Conversely, a low specificity could lead to an overdiagnosis of the disease, potentially subjecting individuals to unnecessary treatments or interventions.
Moreover, in the context of machine learning and artificial intelligence, understanding specificity is vital for building accurate and reliable models. By optimizing for specificity, developers can ensure their models minimize false positives, leading to more precise and trustworthy predictions.
Sensitivity: Capturing the True Positives
Sensitivity, another critical metric in diagnostic testing, refers to the ability of a test to correctly identify individuals who have the condition of interest. In simpler terms, it measures the proportion of true positives out of all individuals who were correctly classified as positive. This metric is a key indicator of a test’s effectiveness in capturing true cases of the condition.
In the medical context, sensitivity is often referred to as the "true positive rate". It represents the probability that a test will correctly identify a person who has the disease as positive. For instance, if a test has a sensitivity of 90%, it means that for every 10 individuals who have the disease, the test will correctly identify 9 of them as having the disease.
Mathematically, sensitivity can be expressed as:
| Sensitivity | True Positive |
|---|---|
| Sensitivity = | TP / (TP + FN) |
Here, TP represents the number of true positives, and FN represents the number of false negatives. This equation underscores the direct relationship between sensitivity and the accuracy of a test in identifying individuals who truly have the disease.
In the realm of predictive modeling, sensitivity plays a pivotal role in capturing true positives. A high sensitivity value indicates a lower likelihood of false negatives, which is crucial in scenarios where false negatives could have severe consequences. For example, in disease detection, a test with high sensitivity is desirable to ensure that as many individuals with the disease as possible are correctly identified.
The Significance of Sensitivity in Healthcare
Sensitivity is not just a statistical measure; it has profound implications for healthcare and patient outcomes. In diagnostic tests, a high sensitivity can lead to early detection and timely intervention, potentially improving patient prognosis and reducing morbidity and mortality rates. This is particularly critical for diseases where early detection is key to successful treatment.
For instance, consider a diagnostic test for a serious infectious disease. A high sensitivity ensures that a negative result is more likely to be an accurate indicator of the absence of the disease. Conversely, a low sensitivity could lead to an underdiagnosis of the disease, potentially delaying necessary treatments and interventions.
Furthermore, in the context of machine learning and artificial intelligence, optimizing for sensitivity can be crucial for building accurate and reliable models. By focusing on sensitivity, developers can ensure their models minimize false negatives, leading to more robust and effective predictions, especially in critical healthcare applications.
The Balancing Act: Specificity vs. Sensitivity
While specificity and sensitivity are both critical metrics in diagnostic testing, they often present a trade-off. Increasing the sensitivity of a test often leads to a decrease in specificity, and vice versa. This trade-off is a fundamental aspect of diagnostic test design and interpretation.
Consider a diagnostic test for a disease with two possible outcomes: positive or negative. A positive result indicates the presence of the disease, while a negative result indicates the absence. In this scenario, a high sensitivity test would aim to correctly identify as many individuals with the disease as possible (true positives), even if it means a higher number of false positives (individuals without the disease incorrectly identified as having it). On the other hand, a high specificity test would prioritize correctly identifying individuals without the disease (true negatives), potentially leading to a higher number of false negatives (individuals with the disease incorrectly identified as not having it).
This trade-off is often depicted on the ROC curve, where a test's performance is represented by a point on the curve. The position of this point indicates the balance between sensitivity and specificity. Moving the point towards the top left corner of the ROC curve (perfect classification) represents a test with high sensitivity and specificity. However, in practice, achieving a test with perfect classification is often challenging, and a balance between sensitivity and specificity must be struck to optimize diagnostic accuracy.
Navigating the Trade-off: Practical Considerations
In real-world scenarios, the choice between prioritizing sensitivity or specificity often depends on the context and the potential consequences of false positives and false negatives. For instance, in disease screening, a high sensitivity test might be preferred to ensure that as many cases of the disease are detected as possible, even if it means a higher number of false positives. This is particularly true for diseases with serious consequences where early detection is crucial.
On the other hand, in diagnostic tests where false positives could lead to unnecessary interventions or treatments, a high specificity test might be preferred. This is often the case in follow-up tests after an initial positive result, where the goal is to confirm the presence of the disease with a high degree of certainty.
Additionally, the cost and ease of performing the test can also influence the decision. For instance, a highly sensitive but expensive or invasive test might not be practical for widespread use, whereas a less sensitive but more affordable and accessible test might be preferred for initial screening.
Conclusion: Understanding the ROC Landscape

In the complex landscape of diagnostic testing and predictive modeling, the concepts of specificity and sensitivity are indispensable tools. They provide a nuanced understanding of a test’s or model’s performance, guiding decision-making and shaping clinical practice.
By comprehending the trade-off between specificity and sensitivity, healthcare professionals and researchers can make informed decisions about test selection and interpretation. This understanding is particularly crucial in the era of precision medicine and data-driven healthcare, where diagnostic accuracy and predictive modeling play an increasingly vital role.
As we navigate the intricate world of ROC analysis, the importance of specificity and sensitivity cannot be overstated. These metrics offer a lens through which we can interpret test results, evaluate model performance, and make informed decisions that directly impact patient care and outcomes. With a deep understanding of these concepts, we can continue to advance the frontiers of healthcare and improve patient lives.
How is specificity calculated in diagnostic tests?
+Specificity is calculated using the formula: Specificity = True Negatives / (True Negatives + False Positives). This formula highlights the proportion of true negatives out of all individuals who were correctly classified as negative.
What are the implications of a high sensitivity test in healthcare?
+A high sensitivity test in healthcare can lead to early detection and timely intervention for diseases, potentially improving patient prognosis and reducing morbidity and mortality rates. It ensures that as many individuals with the disease as possible are correctly identified, even if it means a higher number of false positives.
How do specificity and sensitivity impact the ROC curve?
+Specificity and sensitivity are key components of the ROC curve. The ROC curve represents the trade-off between these two metrics, with a point on the curve indicating the balance between sensitivity and specificity for a given test. The closer the point is to the top left corner of the ROC curve, the better the test’s performance.



