Significant Digits Rules Examples
Understanding significant digits, also known as significant figures, is crucial in scientific and mathematical contexts, as they represent the precision and accuracy of measurements and calculations. The rules governing significant digits ensure consistent and meaningful data representation. In this comprehensive guide, we will delve into the concept of significant digits, explore the rules and conventions associated with them, provide numerous examples, and offer valuable insights to enhance your understanding and application of this essential topic.
The Significance of Significant Digits

Significant digits, often abbreviated as sig figs, are the digits in a number that convey meaningful information about the quantity being measured or calculated. They indicate the level of precision or uncertainty in a measurement. By following specific rules, we can effectively communicate the reliability of our data and facilitate accurate comparisons and calculations.
Rules for Identifying Significant Digits

Determining significant digits involves understanding a set of straightforward rules. Here’s a breakdown of these rules, along with illustrative examples:
Rule 1: Non-Zero Digits
All non-zero digits in a number are considered significant. For instance, in the number 45.62, all four digits are significant: 4, 5, 6, and 2. This rule emphasizes the importance of every digit in conveying the magnitude of a measurement.
Rule 2: Zeros Between Non-Zero Digits
Zeros sandwiched between non-zero digits are significant. Take the number 105 as an example; the zero between the 1 and 5 is significant. These zeros contribute to the overall precision of the measurement.
Rule 3: Leading Zeros
Leading zeros, those appearing before the first non-zero digit, are not significant. For example, in the number 0.004, the three leading zeros do not add to the significance of the measurement. They merely indicate the position of the decimal point.
Rule 4: Trailing Zeros
Trailing zeros, zeros at the end of a number, are significant if the number contains a decimal point. Consider the number 3.200; the two trailing zeros after the decimal point are significant, indicating a higher level of precision.
Rule 5: Zeros Without a Decimal Point
Zeros without a decimal point are significant only if they are sandwiched between non-zero digits or if they are the only digits in the number. For instance, in 400, the zero is significant as it is sandwiched between the 4 and 0. However, in 5000, the zeros are not significant as they are leading zeros.
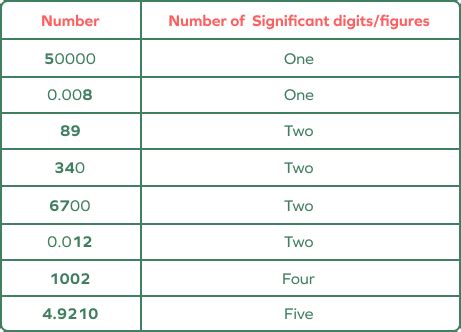
Examples of Significant Digits in Action
Let’s apply these rules to some practical examples to better understand the concept of significant digits:
| Number | Significant Digits |
|---|---|
| 34,200 | 34 |
| 0.0006 | 6 |
| 120.00 | 120 |
| 700,000 | 700 |
| 0.00520 | 520 |
| 1,000,000 | 1 |

In each of these examples, the significant digits are highlighted, demonstrating how the rules apply in different scenarios.
Precision and Accuracy
Significant digits play a pivotal role in understanding the precision and accuracy of measurements. Precision refers to the tightness of data distribution around a central value, while accuracy relates to how close a measurement is to the true value. Significant digits provide a means to quantify and communicate these concepts.
Precision Example
Imagine we have two sets of measurements for the weight of an object. The first set yields the values 12.5, 12.6, and 12.7 grams, while the second set gives 12.500, 12.600, and 12.700 grams. Both sets have the same mean value, but the second set has a higher precision due to the increased number of significant digits.
Accuracy Example
Suppose we measure the length of a table twice, resulting in the values 1.25 meters and 1.26 meters. Although the measurements have different numbers of significant digits, they are both accurate as they closely approximate the true length of the table.
Rounding and Significant Digits

Rounding numbers is a common practice to simplify calculations and convey the appropriate level of precision. When rounding, it’s essential to consider the significant digits to maintain accuracy. Here are some guidelines for rounding numbers:
- Rounding to a Specific Number of Digits: When rounding to a particular number of significant digits, the general rule is to look at the digit immediately to the right of the desired significant digit. If this digit is 5 or greater, increase the preceding digit by 1; if it's less than 5, leave the preceding digit unchanged. For example, rounding 12.356 to three significant digits yields 12.4.
- Rounding Up or Down: In some cases, you may need to round a number up or down to a specific value. For instance, rounding 2.3 to the nearest whole number results in 2, while rounding 2.6 to the nearest whole number gives 3.
Significant Digits in Calculations
When performing calculations, it’s crucial to maintain consistency in the number of significant digits. Here are some guidelines to follow:
- Addition and Subtraction: In addition and subtraction, the result should have the same number of decimal places as the least precise number in the calculation. For example, 12.34 + 4.5 = 16.84, rounded to the nearest thousandth.
- Multiplication and Division: The product or quotient of a multiplication or division should have the same number of significant digits as the least precise factor or divisor. For instance, 2.34 × 5 = 11.7, rounded to the nearest tenth.
Real-World Applications
Significant digits find extensive application in various scientific and engineering disciplines. Here are a few examples:
- Physics: In physics experiments, significant digits help convey the precision of measurements, such as distances, velocities, and forces.
- Chemistry: Chemists use significant digits to represent the accuracy of chemical quantities, concentrations, and reaction rates.
- Engineering: Engineers rely on significant digits to specify the precision of dimensions, tolerances, and material properties in their designs.
- Meteorology: Meteorologists use significant digits to express the accuracy of weather data, including temperature, humidity, and atmospheric pressure.
Conclusion
Significant digits are an essential concept in scientific and mathematical contexts, enabling precise communication of measurement data. By understanding the rules and conventions associated with significant digits, you can accurately represent the precision and accuracy of your measurements and calculations. This guide has provided a comprehensive overview, backed by examples and real-world applications, to enhance your grasp of this fundamental topic.
How do significant digits impact the accuracy of calculations?
+Significant digits directly influence the accuracy of calculations by determining the level of precision allowed in the final result. When performing calculations, the result should have the same number of significant digits as the least precise input value. This ensures that the final answer reflects the precision of the original data.
Can significant digits be different for the same number in different contexts?
+Yes, the number of significant digits can vary depending on the context and the level of precision required. For example, a measurement of 1.23 meters may have three significant digits in one context, but if a higher precision is needed, it could be expressed as 1.230 meters, increasing the number of significant digits to four.
Are significant digits always rounded up or down in calculations?
+In calculations, significant digits are typically rounded to the appropriate number of decimal places. Whether the final digit is rounded up or down depends on the value of the digit immediately to the right. If this digit is 5 or greater, the preceding digit is rounded up; otherwise, it remains unchanged.


