Significant Figures Measurement

Welcome to an exploration of the fascinating world of significant figures in measurement, a critical concept in science and engineering. This comprehensive guide delves into the intricacies of significant figures, their role in data representation, and their impact on the accuracy and precision of measurements. We will navigate through the principles, best practices, and practical applications, ensuring a thorough understanding of this fundamental topic.
Understanding Significant Figures

In the realm of scientific measurements, significant figures, often abbreviated as sig figs, represent a critical aspect of data precision and accuracy. They are the digits in a number that provide meaningful information about the measured quantity. These digits, excluding leading and trailing zeros, carry essential details about the magnitude and precision of a measurement.
The concept of significant figures is fundamental in various scientific fields, including physics, chemistry, engineering, and many others. It ensures that data is communicated accurately and precisely, allowing for meaningful comparisons and analyses. By understanding and applying the rules of significant figures, scientists and engineers can effectively convey the quality of their measurements and facilitate informed decision-making.
The Role of Leading and Trailing Zeros
Leading and trailing zeros are integral to the concept of significant figures. Leading zeros, which appear before the first non-zero digit, are not considered significant. They are merely placeholders and do not impact the value of the measurement. For instance, the number 0.005 has only one significant figure, which is 5. The leading zeros in this case do not add to the precision of the measurement.
Conversely, trailing zeros, which appear after the last non-zero digit, can be significant. These zeros indicate that the measurement has been made to a higher level of precision. For example, the number 12.00 has three significant figures: 1, 2, and 0. The trailing zeros here suggest that the measurement was made with a high degree of precision, potentially to the hundredths place.
| Number | Significant Figures |
|---|---|
| 0.005 | 1 |
| 12.00 | 3 |
| 300 | 1 |
| 57,000 | 2 |
| 0.000006 | 1 |

This table illustrates the concept of significant figures with various examples. Each number is broken down to highlight the significant digits, offering a clear understanding of how these figures are determined.
Rules for Determining Significant Figures
Determining the significant figures in a measurement is governed by a set of rules, which help standardize the process and ensure consistency in data representation. These rules are particularly important when working with large or small numbers, as they provide a clear framework for identifying the digits that carry meaningful information.
Rules for Whole Numbers
When dealing with whole numbers, the rules for significant figures are relatively straightforward. Here are the key guidelines:
- Non-zero Digits: All non-zero digits are considered significant. For example, in the number 4,230, there are three significant figures: 4, 2, and 3.
- Trailing Zeros: Trailing zeros in a whole number are significant only if the number contains a decimal point. For instance, in 4,230., the trailing zero is significant, giving a total of four significant figures.
- Leading Zeros: Leading zeros are never significant. They are simply placeholders and do not add to the precision of the measurement. For example, 00423 has only three significant figures: 4, 2, and 3.
Rules for Decimal Numbers
Decimal numbers, with their inherent precision, follow slightly different rules for determining significant figures. Here’s a breakdown:
- All Digits: In decimal numbers, all digits, including those after the decimal point, are considered significant. For example, 0.056 has three significant figures: 5, 6, and 0.
- Trailing Zeros: Trailing zeros in decimal numbers are always significant. They indicate the precision of the measurement. For instance, 3.400 has four significant figures: 3, 4, 0, and 0.
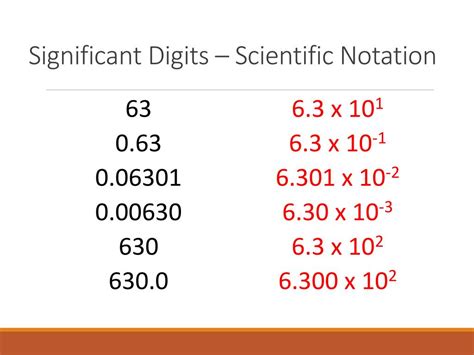
Rules for Scientific Notation
Scientific notation is a powerful tool for representing very large or very small numbers. When using scientific notation, the rules for significant figures are applied to the coefficient, which is the part of the number before the base-10 exponent.
- Coefficient: All digits in the coefficient are considered significant. For example, in 3.456 x 10^4, there are three significant figures: 3, 4, and 5.
- Exponent: The exponent in scientific notation does not affect the significant figures. It simply represents the power of 10, which adjusts the magnitude of the number.
Operations with Significant Figures
When performing calculations with measurements, it’s crucial to consider the impact of significant figures on the final result. Operations such as addition, subtraction, multiplication, and division can affect the precision of the data, and understanding how to manage significant figures in these operations is essential for maintaining accuracy.
Addition and Subtraction
When adding or subtracting measurements, the result should have the same number of decimal places as the measurement with the fewest decimal places. This ensures that the precision of the result aligns with the least precise measurement involved.
For example, consider the addition of 3.456 and 2.2. The number 2.2 has only one decimal place, so the result should also have one decimal place: 5.6.
Multiplication and Division
In multiplication and division, the significant figures in the result are determined by the measurement with the fewest significant figures. This rule ensures that the precision of the result is not exaggerated.
For instance, if we multiply 3.456 by 2.2, the result should have three significant figures, as 2.2 has only two significant figures. The calculated result, 7.6032, rounded to three significant figures, is 7.60.
Rounding and Estimation
Rounding and estimation are essential techniques for managing significant figures, especially when dealing with large or complex calculations. These methods help simplify data and ensure that the results are presented with the appropriate level of precision.
Rounding to a Specific Precision
Rounding a number to a specific precision involves adjusting the digits to the desired level of detail. This process ensures that the significant figures in the result align with the desired level of precision.
For example, rounding 3.456 to two significant figures would result in 3.5. The original number's precision is preserved, but the result is simplified for easier interpretation.
Estimation Techniques
Estimation is a valuable tool for quickly approximating results, especially in complex calculations or when working with large datasets. It involves making educated guesses about the outcome, often by rounding off digits or using mental math shortcuts.
For instance, when estimating the product of 3.456 and 2.2, one might round 3.456 to 3 and 2.2 to 2, resulting in an estimated product of 6. While this estimation may not be exact, it provides a quick and useful approximation.
Impact of Significant Figures on Data Precision

The concept of significant figures is intimately linked to data precision. Precision refers to the level of detail or refinement in a measurement, and significant figures are a direct indicator of this precision.
Precision and Accuracy
Precision and accuracy are often used interchangeably, but they represent distinct aspects of measurement quality. Precision refers to the consistency or repeatability of measurements, while accuracy refers to how closely the measured value aligns with the actual, true value.
Significant figures play a crucial role in ensuring precision. By adhering to the rules of significant figures, scientists and engineers can consistently represent measurements with the appropriate level of detail, maintaining the integrity of their data.
Real-World Applications
The impact of significant figures extends far beyond theoretical considerations. In practical scenarios, such as scientific research, engineering design, or quality control, the precision conveyed by significant figures can have significant implications.
For instance, in the pharmaceutical industry, the precision of measurements is critical for drug formulation and dosage. Misinterpreting significant figures could lead to incorrect drug concentrations, potentially impacting patient safety and treatment effectiveness.
Best Practices for Working with Significant Figures
Working with significant figures requires a careful and methodical approach. Here are some best practices to ensure accuracy and precision in your measurements:
- Understand the Context: Before performing any calculations, understand the context of the measurements. This includes knowing the level of precision required for the specific application or experiment.
- Identify Significant Figures: Carefully identify the significant figures in each measurement. This step is crucial for ensuring that the precision of the data is maintained throughout calculations.
- Apply Consistent Rules: Consistently apply the rules for determining significant figures. Whether you're dealing with whole numbers, decimals, or scientific notation, ensure that the same principles are applied across the board.
- Use Appropriate Rounding: Round off numbers to the appropriate level of precision when necessary. This helps simplify calculations and ensures that the final result aligns with the desired level of detail.
- Document Your Work: Keep detailed records of your calculations, including the original measurements, intermediate results, and final outcomes. This documentation ensures transparency and allows for easy verification of your work.
Conclusion: Mastering Significant Figures
Mastering the concept of significant figures is a crucial step towards proficiency in scientific and engineering disciplines. By understanding and applying the principles outlined in this guide, you can effectively manage the precision and accuracy of your measurements.
Significant figures are more than just a set of rules; they are a fundamental tool for communicating the quality of your data. Whether you're conducting research, designing a product, or analyzing data, the careful consideration of significant figures ensures that your work is grounded in rigorous scientific principles.
As you continue your journey in science and engineering, remember that precision and accuracy are not just technical terms, but fundamental values that underpin the integrity of your work. With a solid grasp of significant figures, you'll be well-equipped to navigate the complex world of measurements with confidence and precision.
Frequently Asked Questions
How do I determine the significant figures in a whole number?
+To determine the significant figures in a whole number, consider all non-zero digits as significant. Leading zeros are never significant, while trailing zeros are significant only if the number contains a decimal point.
What are the rules for significant figures in decimal numbers?
+In decimal numbers, all digits, including those after the decimal point, are considered significant. Trailing zeros in decimal numbers are always significant and indicate the precision of the measurement.
How do I handle significant figures in scientific notation?
+In scientific notation, focus on the coefficient. All digits in the coefficient are significant. The exponent, which represents the power of 10, does not affect the significant figures.
What’s the rule for significant figures in addition and subtraction?
+When adding or subtracting measurements, the result should have the same number of decimal places as the measurement with the fewest decimal places. This ensures that the precision of the result aligns with the least precise measurement involved.
How are significant figures determined in multiplication and division?
+In multiplication and division, the significant figures in the result are determined by the measurement with the fewest significant figures. This rule ensures that the precision of the result is not exaggerated.