Svm Kernel Figures
Unveiling the Power of SVM Kernel Functions: A Comprehensive Guide

Support Vector Machines (SVM) are a powerful tool in the field of machine learning, offering a robust approach to classification and regression tasks. At the heart of SVM's versatility lie its kernel functions, which enable the model to handle complex, non-linear decision boundaries. This comprehensive guide aims to demystify SVM kernel functions, exploring their principles, types, and practical applications. Through a deep dive into this essential component of SVMs, we will uncover the keys to unlocking the full potential of these machine learning models.
Understanding the Fundamentals: SVM Kernel Functions

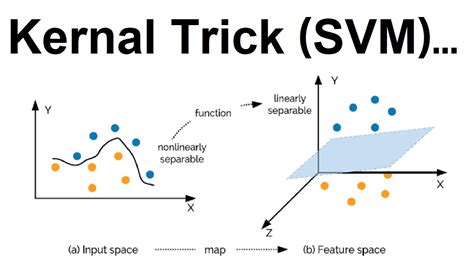
SVM kernel functions are mathematical functions that transform the original feature space into a higher-dimensional space, making it possible to separate data points that are not linearly separable in the original space. This transformation allows SVMs to find a hyperplane that optimally separates the data, even when the data exhibits complex, non-linear patterns.
The fundamental concept behind SVM kernel functions is the kernel trick, which allows us to compute the inner product in a higher-dimensional space without explicitly mapping the data into that space. This trick significantly simplifies the computation and enables SVMs to handle high-dimensional data efficiently.
The choice of kernel function plays a pivotal role in the performance and applicability of SVMs. Different kernel functions offer varying levels of complexity and flexibility, catering to different types of data and problem domains. The most common SVM kernel functions include the linear kernel, polynomial kernel, radial basis function (RBF) kernel, and sigmoid kernel. Each of these functions has its unique characteristics and is suited for specific scenarios.
Linear Kernel
The linear kernel is the simplest of all SVM kernels. It is essentially the dot product of two feature vectors, representing a linear decision boundary in the original feature space. The linear kernel is best suited for datasets that are already linearly separable and where the relationship between the input variables and the output is linear.
| Kernel Type | Mathematical Expression |
|---|---|
| Linear Kernel | k(x, y) = x·y |

Polynomial Kernel
The polynomial kernel is a more flexible option, allowing for the representation of non-linear decision boundaries. It transforms the original feature space into a higher-dimensional space by raising each feature to a specified power. The polynomial kernel is often used when the relationship between the input variables and the output is non-linear, and it can capture more complex patterns in the data.
| Kernel Type | Mathematical Expression |
|---|---|
| Polynomial Kernel | k(x, y) = (x·y + c) ^ d |
Where c is a constant and d is the degree of the polynomial.
Radial Basis Function (RBF) Kernel
The RBF kernel, also known as the Gaussian kernel, is one of the most popular SVM kernels. It transforms the data into an infinite-dimensional space and finds a non-linear decision boundary by considering the similarity between data points. The RBF kernel is particularly useful when the data exhibits a Gaussian-like distribution or when the decision boundary needs to be smooth and flexible.
| Kernel Type | Mathematical Expression |
|---|---|
| RBF Kernel | k(x, y) = exp(-γ||x - y||^2) |
Where γ is a tuning parameter that controls the width of the kernel.
Sigmoid Kernel
The sigmoid kernel is inspired by the activation function used in neural networks. It maps the data into a high-dimensional space, creating a non-linear decision boundary. The sigmoid kernel is particularly useful when the data exhibits a complex, non-linear relationship, and it can capture intricate patterns.
| Kernel Type | Mathematical Expression |
|---|---|
| Sigmoid Kernel | k(x, y) = tanh(a·x·y + b) |
Where a and b are tuning parameters.
Practical Applications and Case Studies
SVM kernel functions find applications across various domains, including image classification, natural language processing, and bioinformatics. Let's explore a few real-world examples to understand the practical implications of SVM kernel functions.
Image Classification with SVM Kernels
In image classification tasks, SVMs with kernel functions have been widely used to distinguish between different types of images. For instance, in a medical imaging context, SVMs with an RBF kernel can effectively classify X-ray images into different categories, such as normal vs. abnormal, or cancerous vs. non-cancerous.
The ability of the RBF kernel to handle non-linear decision boundaries is particularly advantageous in image classification, where the underlying patterns might not be linear. By transforming the image features into a higher-dimensional space, SVMs with the RBF kernel can capture intricate relationships and improve classification accuracy.
Natural Language Processing: Text Classification
SVM kernel functions have also proven their worth in natural language processing tasks, particularly in text classification. For example, in sentiment analysis, an SVM with a polynomial kernel can be used to classify text documents into positive, negative, or neutral sentiment categories.
The polynomial kernel's ability to capture non-linear relationships between words and their contexts makes it well-suited for sentiment analysis. By mapping the text data into a higher-dimensional space, the SVM can identify complex patterns and nuances in the text, leading to more accurate sentiment classifications.
Bioinformatics: Gene Expression Analysis
In the field of bioinformatics, SVM kernel functions have been applied to gene expression analysis. Here, SVMs with an RBF kernel can classify genes into different functional categories based on their expression patterns.
The RBF kernel's flexibility and ability to handle high-dimensional data make it an ideal choice for gene expression analysis. By transforming the gene expression data into a higher-dimensional space, the SVM can capture intricate relationships between genes and their functions, aiding in the identification of biologically significant patterns.
Choosing the Right Kernel Function: A Comparative Analysis
The selection of an appropriate kernel function is a critical step in the SVM modeling process. The choice depends on the nature of the data, the problem domain, and the specific requirements of the task at hand. Let's delve into a comparative analysis of the different SVM kernel functions to help guide this decision-making process.
Linear Kernel vs. Non-Linear Kernels
The linear kernel is simple and efficient, making it a good choice for datasets that are already linearly separable. However, for datasets with complex, non-linear patterns, the linear kernel might not be sufficient. In such cases, non-linear kernels, such as the polynomial, RBF, or sigmoid kernels, are more suitable.
Non-linear kernels offer increased flexibility and the ability to capture intricate relationships in the data. However, they also introduce more complexity and computational overhead, making the choice of kernel a trade-off between model complexity and computational efficiency.
Polynomial Kernel vs. RBF Kernel
The polynomial kernel and the RBF kernel are both non-linear kernels, but they have distinct characteristics. The polynomial kernel is more flexible, as it allows for a wider range of non-linear decision boundaries. However, it can also lead to overfitting if not carefully tuned.
On the other hand, the RBF kernel is more versatile and generally more robust to overfitting. It can capture smooth, non-linear decision boundaries and is well-suited for high-dimensional data. The RBF kernel is often the go-to choice when the data exhibits a Gaussian-like distribution or when a smooth decision boundary is preferred.
Sigmoid Kernel vs. Other Non-Linear Kernels
The sigmoid kernel is inspired by neural networks and is designed to capture complex, non-linear relationships. It can be particularly useful when the data exhibits intricate patterns that other non-linear kernels might struggle to capture.
However, the sigmoid kernel can be more challenging to tune and might require more computational resources. In comparison to the polynomial and RBF kernels, the sigmoid kernel is often used when the problem domain specifically calls for a neural network-inspired approach or when the data exhibits highly non-linear patterns.
Tuning SVM Kernel Parameters: A Practical Guide

Tuning the parameters of SVM kernel functions is a crucial step to ensure optimal model performance. The choice of kernel function and its associated parameters can significantly impact the model's accuracy, generalization, and computational efficiency.
The most common parameters to tune for SVM kernel functions include the kernel type, the regularization parameter C, and the kernel-specific parameters (e.g., γ for the RBF kernel, d for the polynomial kernel, etc.). These parameters control the trade-off between model complexity and generalization, and their optimal values depend on the specific dataset and problem domain.
Kernel Type Selection
The first step in tuning SVM kernel parameters is to select the appropriate kernel type. This decision is based on the nature of the data and the problem domain. As discussed earlier, linear kernels are suitable for linearly separable datasets, while non-linear kernels are needed for more complex, non-linear patterns.
Regularization Parameter C
The regularization parameter C controls the trade-off between maximizing the margin (the distance between the hyperplane and the support vectors) and minimizing classification errors. A larger value of C emphasizes the importance of correctly classifying training samples, potentially leading to overfitting. Conversely, a smaller value of C focuses more on maximizing the margin, which can improve generalization but might lead to underfitting.
The optimal value of C depends on the dataset and the specific problem. It is often determined through cross-validation, where different values of C are tested, and the one that yields the best performance is chosen.
Kernel-Specific Parameters
Each SVM kernel function has its own set of parameters that need to be tuned. For instance, the RBF kernel has the γ parameter, which controls the width of the kernel and influences the shape of the decision boundary. Similarly, the polynomial kernel has the d parameter, which determines the degree of the polynomial and the complexity of the decision boundary.
Tuning these kernel-specific parameters is crucial for achieving the best model performance. Again, cross-validation is often used to find the optimal values for these parameters, ensuring that the model generalizes well to unseen data.
Future Trends and Advancements in SVM Kernel Functions
The field of SVM kernel functions is continually evolving, with researchers exploring new kernel designs and optimization techniques. Some of the emerging trends and advancements include:
- Composite Kernels: Composite kernels combine multiple base kernels to create more complex decision boundaries. This approach allows for greater flexibility and the ability to capture a wider range of patterns in the data.
- Deep Learning-Inspired Kernels: With the rise of deep learning, researchers are exploring ways to incorporate deep learning concepts into SVM kernels. This includes the development of deep neural network-inspired kernels and the integration of convolutional neural networks with SVMs.
- Adaptive Kernels: Adaptive kernels adjust their parameters based on the characteristics of the data. These kernels can automatically tune their behavior to better fit the data, leading to improved generalization and robustness.
- Kernel Optimization Techniques: Researchers are developing new optimization algorithms specifically tailored for SVM kernel functions. These algorithms aim to improve the efficiency of kernel computation and parameter tuning, making SVMs more practical for large-scale datasets.
As the field of machine learning advances, SVM kernel functions will continue to evolve, offering even more powerful and flexible tools for tackling complex classification and regression problems.
Conclusion
SVM kernel functions are a cornerstone of Support Vector Machines, enabling these models to handle a wide range of machine learning tasks. By understanding the principles, types, and practical applications of SVM kernel functions, we can harness their full potential and apply them effectively to various real-world problems.
The choice of kernel function is a critical decision, and the proper selection and tuning of kernel parameters can significantly impact the model's performance. As the field of machine learning continues to evolve, the development of new and innovative kernel functions will further enhance the capabilities of SVMs, opening up new avenues for exploration and discovery.
What is the main purpose of SVM kernel functions?
+SVM kernel functions transform the original feature space into a higher-dimensional space, enabling SVMs to find an optimal hyperplane that separates data points effectively, even when the data is not linearly separable.
Which kernel function should I use for linearly separable data?
+For linearly separable data, the linear kernel is the simplest and most efficient choice. It represents a linear decision boundary in the original feature space.
When should I use the polynomial kernel function?
+The polynomial kernel is suitable for datasets with non-linear patterns. It transforms the data into a higher-dimensional space, allowing for more complex decision boundaries. It is often used when the relationship between input variables and output is non-linear.
What are the advantages of the RBF kernel function?
+The RBF kernel is versatile and robust. It can handle high-dimensional data and finds smooth, non-linear decision boundaries. It is particularly useful when the data exhibits a Gaussian-like distribution or when a smooth decision boundary is preferred.
How do I choose between different SVM kernel functions?
+The choice of kernel function depends on the nature of the data and the problem domain. Linear kernels are suitable for linearly separable data, while non-linear kernels like polynomial, RBF, and sigmoid kernels are needed for more complex, non-linear patterns. Experimentation and cross-validation are often used to find the most suitable kernel for a specific task.



