Weighted Probability
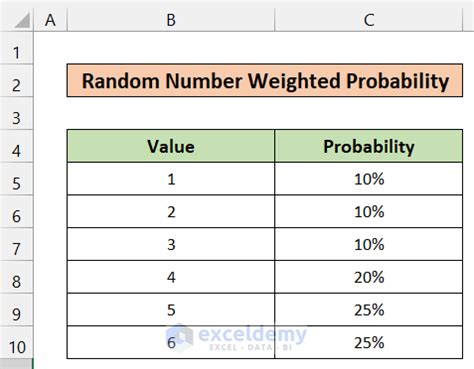
The concept of weighted probability is a fundamental aspect of probability theory, with applications across various fields including mathematics, statistics, artificial intelligence, and data science. It provides a powerful framework for making informed decisions and predictions based on the likelihood of different outcomes. In this comprehensive guide, we will delve into the intricacies of weighted probability, exploring its principles, practical applications, and real-world examples.
Understanding Weighted Probability
Weighted probability extends the traditional notion of probability by assigning different weights or importance to individual events or outcomes. While classical probability treats all outcomes as equally likely, weighted probability recognizes that certain outcomes may be more desirable, more probable, or carry more significance than others.
In essence, weighted probability allows us to incorporate our knowledge, preferences, or available data into the calculation of probabilities. By doing so, we can make more accurate predictions and optimize decision-making processes. The weights assigned to each outcome reflect the relative importance or likelihood associated with that outcome.
Mathematically, the weighted probability of an event A is calculated as the sum of the products of each outcome's probability and its corresponding weight. Let's denote the probability of outcome i as P(i) and its weight as W(i). The weighted probability WP(A) can then be expressed as:
WP(A) = P(1) * W(1) + P(2) * W(2) + ... + P(n) * W(n)
Here, n represents the total number of possible outcomes. This formula allows us to calculate the overall weighted probability by considering the individual probabilities and their respective weights.
Key Applications of Weighted Probability
Weighted probability finds extensive use in various domains, each presenting unique challenges and opportunities. Here are some key applications where weighted probability plays a pivotal role:
- Risk Assessment and Decision Making: In fields like finance, insurance, and project management, weighted probability is employed to assess risks and make informed decisions. By assigning weights to different risk factors or outcomes, professionals can quantify and manage uncertainties effectively.
- Artificial Intelligence and Machine Learning: AI systems often utilize weighted probability to make predictions and optimize their performance. For instance, in natural language processing, weights can be assigned to different word combinations or phrases to improve the accuracy of language models.
- Healthcare and Diagnosis: Medical professionals use weighted probability to diagnose diseases and recommend treatments. By considering various symptoms, test results, and patient histories, they can calculate the likelihood of different conditions and provide personalized healthcare solutions.
- Marketing and Customer Analytics: In the business world, weighted probability is a valuable tool for understanding customer behavior and preferences. By analyzing customer data and assigning weights to different factors, marketers can make data-driven decisions to enhance customer engagement and satisfaction.
- Environmental and Ecological Modeling: Scientists and researchers employ weighted probability to model complex ecological systems and predict the impact of various factors on ecosystems. By assigning weights to different environmental variables, they can assess the likelihood of ecological changes and develop sustainable solutions.
Practical Example: Weather Forecasting
Let’s consider a practical scenario to illustrate the application of weighted probability: weather forecasting.
Imagine a weather prediction model that aims to forecast the probability of rain for a particular city. The model considers various factors such as historical weather data, current atmospheric conditions, and meteorological patterns. Each of these factors carries a certain weight or importance in determining the likelihood of rain.
| Factor | Probability | Weight |
|---|---|---|
| Historical Rainfall | 0.4 | 0.3 |
| Cloud Cover | 0.6 | 0.2 |
| Atmospheric Pressure | 0.2 | 0.4 |
| Wind Speed | 0.1 | 0.1 |

In this example, the weights assigned to each factor reflect their relative importance in predicting rainfall. By multiplying the probability of each factor by its weight and summing up the results, we can obtain the weighted probability of rain for the given city.
WP(Rain) = 0.4 * 0.3 + 0.6 * 0.2 + 0.2 * 0.4 + 0.1 * 0.1 = 0.29
Based on this calculation, the weighted probability of rain is approximately 0.29, indicating a moderate likelihood of rainfall.
Challenges and Considerations
While weighted probability offers powerful capabilities, it is essential to acknowledge certain challenges and considerations:
- Subjectivity: The assignment of weights often involves subjective judgment or expertise. Different individuals or organizations may have varying perspectives on the importance of certain outcomes, leading to potential discrepancies in weighted probability calculations.
- Data Availability: Weighted probability relies on accurate and representative data. In scenarios where data is limited or biased, the calculated weights may not accurately reflect the underlying probabilities, leading to potential inaccuracies in predictions.
- Interpretation and Communication: Communicating the results of weighted probability calculations to stakeholders or decision-makers can be challenging. It is crucial to provide clear explanations and visualizations to ensure proper understanding and interpretation of the weighted probabilities.
Future Implications and Advancements
The field of weighted probability continues to evolve, driven by advancements in technology, data analysis, and machine learning. Here are some future implications and potential advancements:
- Automated Weight Assignment: As machine learning algorithms become more sophisticated, they can assist in automating the process of weight assignment. By analyzing vast amounts of data and identifying patterns, these algorithms can learn to assign weights more accurately and adaptively.
- Integration with Big Data Analytics: With the exponential growth of data, weighted probability can play a crucial role in extracting meaningful insights. By incorporating weighted probability techniques into big data analytics frameworks, organizations can make more informed decisions based on comprehensive and weighted data analysis.
- Personalized Weighting: Weighted probability has the potential to become more personalized. By considering individual preferences, behaviors, and historical data, systems can assign weights tailored to specific users or contexts, leading to more accurate and personalized predictions and recommendations.
Conclusion
Weighted probability is a versatile and powerful tool that enables us to make more informed decisions and predictions by incorporating the importance or likelihood of different outcomes. Its applications span across diverse fields, showcasing its relevance and impact. By understanding the principles and considerations of weighted probability, professionals and researchers can leverage this concept to drive innovation, optimize processes, and enhance decision-making capabilities.
How does weighted probability differ from traditional probability theory?
+Weighted probability extends traditional probability theory by allowing for the assignment of weights to individual outcomes. While classical probability treats all outcomes as equally likely, weighted probability recognizes that certain outcomes may be more important or probable, leading to more accurate predictions.
What are some common challenges in determining weights for different outcomes?
+Determining weights can be challenging due to subjectivity and data availability. Subjective judgment plays a role in assigning weights based on personal expertise or preferences. Additionally, limited or biased data can lead to inaccurate weight assignments. It is crucial to consider diverse perspectives and utilize representative data to ensure accurate weights.
Can weighted probability be applied to all decision-making processes?
+Weighted probability is applicable to a wide range of decision-making processes, especially in scenarios where outcomes have varying degrees of importance or likelihood. However, it may not be suitable for situations where all outcomes are equally likely or when the underlying probabilities are unknown.



